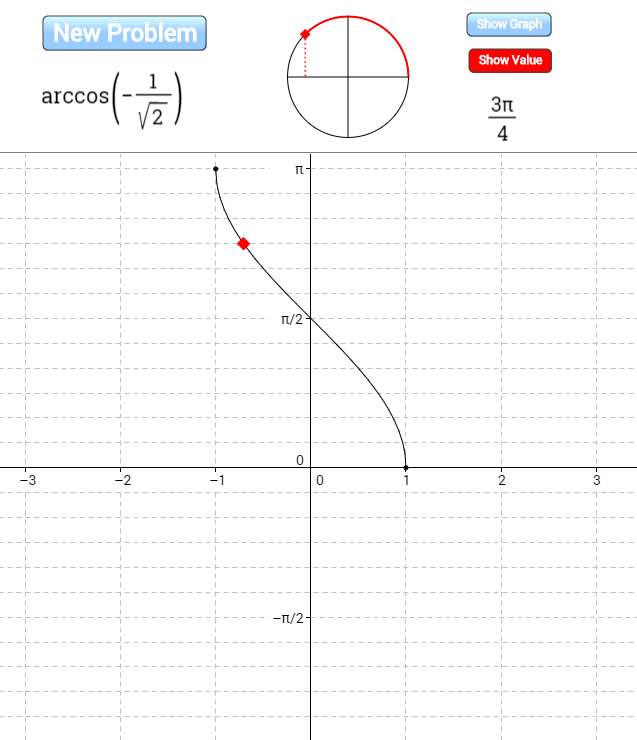
 I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.
I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.
Saturday, May 2, 2015
Evaluating Inverse Trig Expressions
 I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.
I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.
Monday, March 30, 2015
Variation on John Golden's GeoGebra Ferris Wheel
 I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.
I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.We had a great discussion in precalculus class today based on a single randomly generated wheel. We went wherever student questions and answers took us and ended up covering lots of ground. The particularly interesting stuff from my perspective came when those who saw the graph as a shifted sine wave were fighting it out with those who saw it as a shifted cosine wave and those who saw it as a flipped cosine wave. Finally lots of people were seeing lots of ways that they might write an equation for a sinusoidal wave. At the very end of class we generated a new wheel and everyone tried to write a function to go along with it. Class was over and people were pleading, "Please--try my equation!"
Saturday, March 28, 2015
SolveMe Mobiles
 The puzzles at SolveMe Mobiles are linear equations disguised as perfectly balanced mobiles. The early puzzles are simple while the later ones require solving systems of equations. The interface is elegant. Drag a beam to have the corresponding equation appear. Drag a shape that's on both sides of an equation to subtract it. Drag a common factor to divide by it. Substitute by dragging a shape that you've isolated on one side of an equation to somewhere else it appears. Create your own mobiles. Play without creating an account or create an account to save your progress and creations. (No email is required to create an account, though those over 13 may include an email for the purposes of password reset.)
The puzzles at SolveMe Mobiles are linear equations disguised as perfectly balanced mobiles. The early puzzles are simple while the later ones require solving systems of equations. The interface is elegant. Drag a beam to have the corresponding equation appear. Drag a shape that's on both sides of an equation to subtract it. Drag a common factor to divide by it. Substitute by dragging a shape that you've isolated on one side of an equation to somewhere else it appears. Create your own mobiles. Play without creating an account or create an account to save your progress and creations. (No email is required to create an account, though those over 13 may include an email for the purposes of password reset.)
Sunday, March 22, 2015
Rotational and Reflectional Symmetry
 I used GeoGebra to create this applet for exploring the rotational and reflectional symmetry of a variety of images.
I used GeoGebra to create this applet for exploring the rotational and reflectional symmetry of a variety of images.
Friday, March 20, 2015
Euclid: The Game
 Complete with a high score list, Euclid: The Game, created by Kasper Peulen using GeoGebra, presents you with a series of compass and straightedge challenges which get progressively more difficult as you move through the levels. You earn a gold medal for completing a level in the minimum number of moves. See if you can get all the way from constructing an equilateral triangle to inscribing a pentagon in a circle!
Complete with a high score list, Euclid: The Game, created by Kasper Peulen using GeoGebra, presents you with a series of compass and straightedge challenges which get progressively more difficult as you move through the levels. You earn a gold medal for completing a level in the minimum number of moves. See if you can get all the way from constructing an equilateral triangle to inscribing a pentagon in a circle!
Asymptotes of Rational Functions.
 Asymptotes of Rational Functions is a GeoGebra construction designed to help people explore the relationship between the equation of a rational function and its graph. You choose the rational function you'd like to explore. Here's a story of something neat that happened when I used it in class.
Asymptotes of Rational Functions is a GeoGebra construction designed to help people explore the relationship between the equation of a rational function and its graph. You choose the rational function you'd like to explore. Here's a story of something neat that happened when I used it in class.Thursday, March 19, 2015
Finding Equations of Polynomial and Rational Functions
 I created this activity with Desmos. Graphs of several polynomial and rational functions are provided. The goal is to find the equation of each. It's self-checking in that when you type in the right equation your graph will match the given graph.
I created this activity with Desmos. Graphs of several polynomial and rational functions are provided. The goal is to find the equation of each. It's self-checking in that when you type in the right equation your graph will match the given graph.