Unit Circle Practice

Sam Shah's applet for practicing finding special angles on the unit circle and their sines and cosines

Square Pyramid: Underlying Anatomy

From Tim Brezinski

Domain of a Function defined by a Composition

I created this GeoGebra

applet to help with visualization of the domain of a function defined by a composition.

Snail's Trail Quilt Square

I created this GeoGebra applet based on a quilt square pattern to use in a precalculus class as a visual introduction to the sum of an infinite geometric series. A nice accompaniment is this applet from Irina Boyadzhiev. I also created a Desmos activity with a focus on asking questions which incorporates these two applets.

Visualizing radians

Sam Shah shared a GeoGebra applet created by a colleage of his which does a beautiful job of demonstrating what a radian is. He wrote about it here. I made minor modifications, mostly so that the word radian doesn't actually appear. Here's that slightly modified version.

Evaluating Inverse Trig Expressions

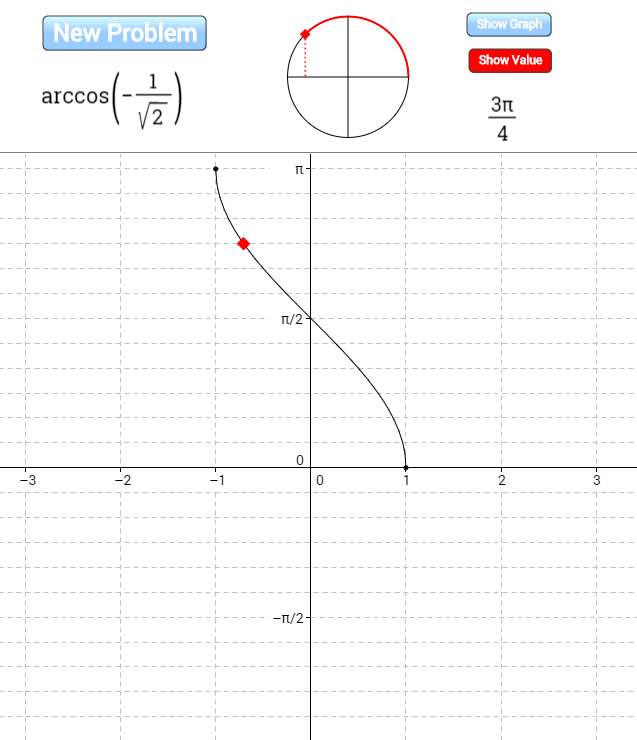I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.

Variation on John Golden's GeoGebra Ferris Wheel

I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.

We had a great discussion in precalculus class today based on a single randomly generated wheel. We went wherever student questions and answers took us and ended up covering lots of ground. The particularly interesting stuff from my perspective came when those who saw the graph as a shifted sine wave were fighting it out with those who saw it as a shifted cosine wave and those who saw it as a flipped cosine wave. Finally lots of people were seeing lots of ways that they might write an equation for a sinusoidal wave. At the very end of class we generated a new wheel and everyone tried to write a function to go along with it. Class was over and people were pleading, "Please--try my equation!"

Rotational and Reflectional Symmetry

I used GeoGebra to create this applet for exploring the rotational and reflectional symmetry of a variety of images.

Euclid: The Game

Complete with a high score list, Euclid: The Game, created by Kasper Peulen using GeoGebra, presents you with a series of compass and straightedge challenges which get progressively more difficult as you move through the levels. You earn a gold medal for completing a level in the minimum number of moves. See if you can get all the way from constructing an equilateral triangle to inscribing a pentagon in a circle!

Asymptotes of Rational Functions.

Asymptotes of Rational Functions is a GeoGebra construction designed to help people explore the relationship between the equation of a rational function and its graph. You choose the rational function you'd like to explore. Here's a story of something neat that happened when I used it in class.

Intuitive Notion of the Limit - One-Sided Limits

This applet, which is part of Marc Renault's GeoGebra Calculus Applets collection, provides an intuitive introduction to the idea of a limit of a function as x approaches c from the right, left, or both.

The red, green, and blue lines along the x-axis, y-axis and the function which shrink as you decrease δ help with the visualization of motion along the function toward the point where x = c and the corresponding motion toward the limiting values on the axes. Choose from the good library of example functions that are included or enter your own. (I like to start with my own rational function which looks linear but actually has an unseen hole to emphasize from the very beginning the difference between the value of a function and its limit at a point.)

When I used this with a class for the first time, my students asked to see the examples with "Exploding" in the title and they reacted audibly to the motion of the green lines on the y-axis as the function approached its asymptote. My experience has been that when introduced to the idea of limits on a graph there are always a few students who have a lot of difficulty visualizing the various ways in which certain things approach approach other things, and starting with this applet seemed to really help.

Operations on functions graphically

A.B. Cron has created a series of GeoGebra applets that demonstrate operations on functions graphically. You can enter any two functions (f and g) and then, from their graphs, determine points that will be on the graph of, for example, h = f + g. After plotting a number of points, you can check the box to show the graph of h to check your work. The adding functions applet has links to the applets for subtracting, multiplying, dividing, and composition.

(Links updated 7/30/2016)

Finding logs

This is a clean, simple applet by Michael Borcherds that provides practice finding logs. It keeps track of how many you got right on the first try and how much time you've spent. To restart the count, refresh the page.

Inverse functions graphically

Taylor Russell's inverse function applet provides a very nice visualization of the fact that the graph of an inverse function is obtained by switching the x- and y-coordinates of every point. You input the original function, so it is extremely flexible. As an added bonus, you can also plot the reciprocal function and see that it is not the same as the inverse. I used this applet in combination with Emily Alman's Joe the Math Guy comic for my most successful introduction to inverse functions ever.

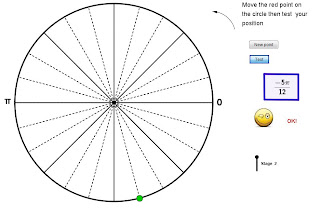
Radian measure practice

This is one of the simpler of a huge number of elegant GeoGebra creations from Daniel Mentrard. (Those available in HTML rather than Java are here.) You're given an angle which is some integer multiple of pi/12 and asked to place it on the appropriate place on a circle. You then push the test button to see if you've placed it correctly. You can choose between "Stage 1" and "Stage 2" problems. Stage 1 has only positive angles. Stage 2 includes negative angles.

Transforming f into g

Note: If you're not seeing both graphics windows on GeoGebraTube, you can download the applet and run it on your desktop.

In this applet (inspired by Steve Phelps' What's My Rule series) you select a parent function, f(x),  from among 10 possibilities and click a button to indicate the maximum number of transformations (up to 4) that you'd like to have performed on f to produce a new function g. You see only one point on g, but you can move the corresponding point on f, to determine the relationship between the two. When you believe you have found the parameters that describe the transformation, you can show the graph of the transformed function that your parameters create and see if the lone point moves along it.

Here's a Java version of the applet.

Ferris Wheel

This is a full-featured and beautifully designed GeoGebra applet from John Golden that allows students to practice fitting parameters to a cosine function which models the height of a ferris wheel car above the ground as a function of time. You can watch the ferris wheel spin as the height curve is generated and it provides an endless source of practice since you can always generate a new ferris wheel.

Napier's Gift

I was inspired by the first chapter of Eli Maor's e:The Story of a Number to create this GeoGebra applet designed to help the user discover how to simplify the process of finding a quotient by subtracting exponents. The idea is both to introduce students to logarithms (though they are never mentioned explicitly) and to help students understand why they were so heralded when they were introduced. The applet is also posted on GeoGebraTube.

Visualizing Radian Measure

Ted Coe's Unwrapping a Circle applet on GeoGebra Tube is a visually powerful way of demonstrating what a radian is. I've also posted a slight modification of the applet optimized for use as a demonstration.

Indiana Puzzle Quilt

This applet was inspired by a quilt square my mother-in-law made. It provides a nice way of visualizing the  the sum of an infinite geometric series.
Check out the pattern in some real quilts, too!

Update 1/5/2017: See the Snail's Trail Quilt Square