Domain of a Function defined by a Composition

I created this GeoGebra

applet to help with visualization of the domain of a function defined by a composition.

Exponential Models Card Sort

Thanks to the ever-innovative-and-tuned-in-to-what-teachers-would-love-to-have Desmos team, I've created an online version of a card sort that I originally developed in paper form to help precalculus students think carefully about the meaning of the parameters in various forms of exponential equations. See this blog post for more detail on the context in which I use this.

Evaluating Inverse Trig Expressions

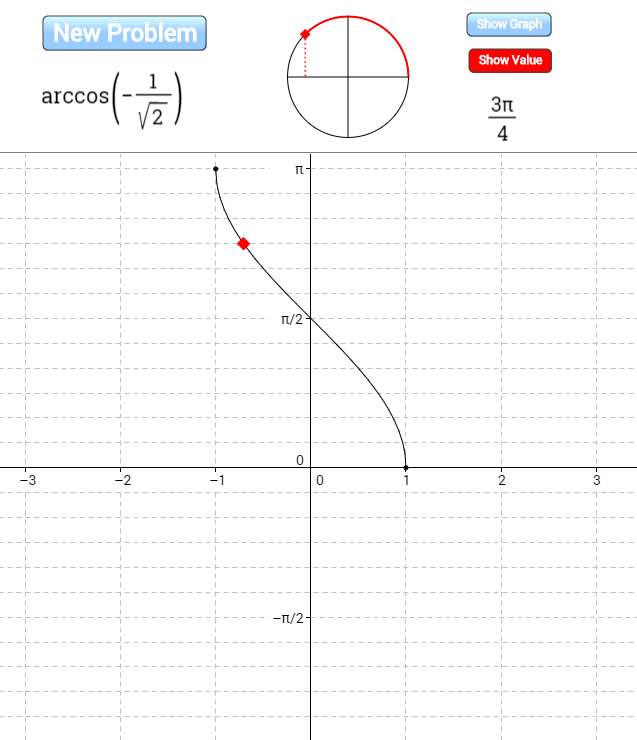I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.

Variation on John Golden's GeoGebra Ferris Wheel

I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.

We had a great discussion in precalculus class today based on a single randomly generated wheel. We went wherever student questions and answers took us and ended up covering lots of ground. The particularly interesting stuff from my perspective came when those who saw the graph as a shifted sine wave were fighting it out with those who saw it as a shifted cosine wave and those who saw it as a flipped cosine wave. Finally lots of people were seeing lots of ways that they might write an equation for a sinusoidal wave. At the very end of class we generated a new wheel and everyone tried to write a function to go along with it. Class was over and people were pleading, "Please--try my equation!"

Finding Equations of Polynomial and Rational Functions

I created this activity with Desmos. Graphs of several polynomial and rational functions are provided. The goal is to find the equation of each. It's self-checking in that when you type in the right equation your graph will match the given graph.

Observe and Ask

This simple Desmos sketch is designed to elicit observations and questions that will lead naturally to an introduction of the ideas of domain and range and an exploration of power functions. I show it to a class without any explanation and as I move the a-slider I ask for questions (which I write on the board, but don't answer). If students want the k-slider moved or if they want to see a particular value of a or k, I oblige. Eventually I ask students to begin trying to answer some of the questions and see where that takes us.

Operations on functions graphically

A.B. Cron has created a series of GeoGebra applets that demonstrate operations on functions graphically. You can enter any two functions (f and g) and then, from their graphs, determine points that will be on the graph of, for example, h = f + g. After plotting a number of points, you can check the box to show the graph of h to check your work. The adding functions applet has links to the applets for subtracting, multiplying, dividing, and composition.

(Links updated 7/30/2016)

Inverse functions graphically

Taylor Russell's inverse function applet provides a very nice visualization of the fact that the graph of an inverse function is obtained by switching the x- and y-coordinates of every point. You input the original function, so it is extremely flexible. As an added bonus, you can also plot the reciprocal function and see that it is not the same as the inverse. I used this applet in combination with Emily Alman's Joe the Math Guy comic for my most successful introduction to inverse functions ever.

Transforming f into g

Note: If you're not seeing both graphics windows on GeoGebraTube, you can download the applet and run it on your desktop.

In this applet (inspired by Steve Phelps' What's My Rule series) you select a parent function, f(x),  from among 10 possibilities and click a button to indicate the maximum number of transformations (up to 4) that you'd like to have performed on f to produce a new function g. You see only one point on g, but you can move the corresponding point on f, to determine the relationship between the two. When you believe you have found the parameters that describe the transformation, you can show the graph of the transformed function that your parameters create and see if the lone point moves along it.

Here's a Java version of the applet.

Ferris Wheel

This is a full-featured and beautifully designed GeoGebra applet from John Golden that allows students to practice fitting parameters to a cosine function which models the height of a ferris wheel car above the ground as a function of time. You can watch the ferris wheel spin as the height curve is generated and it provides an endless source of practice since you can always generate a new ferris wheel.

Daylight Hours Explorer

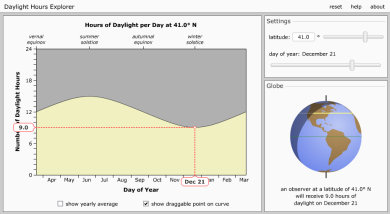This Daylight Hours Explorer is from a fabulous collection of astronomy simulations and animations at the University of Nebraska at Lincoln. Exploring hours of daylight over the course of a year at various locations on the earth is a great way for students to think carefully about parameters of trig functions.

Spinning Out Sine and Cosine

A nice animation from the Wolfram Demonstrations Project showing the relationship between a circle and the graphs of sine and cosine. I like the way the cosine graph is show on its side. I'm going to try using it (after editing it in Mathematica to remove the sine and cosine labels) as an introduction both to the unit circle and the trig graphs. It looks like a good candidate for the technique of showing an animation with no commentary and then asking for student questions, writing them on the board, and asking for answers to/discussion of any of the questions.

Equation of a quadratic

This sleek GeoGebra applet by Michael Borcherds provides practice in determining the equations of quadratic functions from their graphs. Some of the generated parabolas are easier to write equations for in factored form while others are easier to do in (h, k) form. All have leading coefficients of 1. After each function you type in, the function you have given is graphed for comparison with the original and you're told how many you've gotten right and the total amount of time it has taken you.

Graph of a quartic

In this GeoGebra applet, you graph a quartic by setting the values of the four zeros and the leading coefficient. The coordinates of all relative extrema are shown.

Modeling with sine and cosine

In this applet, you look at the graph of a data set (for water level in Cape May, NJ on October 13, 2009) and try to fit a sine function and a cosine function to the data. You can type in your function to see how well it fits the data. Some instruction on how to determine the parameters is provided.

Writing Equations for Sine and Cosine Functions

This applet I created with GeoGebra has 40 problems, which get progressively more difficult, in which the student must write an equation for a graph which is a stretch and/or translation of a sine/cosine graph. To check whether an equation is correct, the student types in the equation and looks at whether the graphs match up.

Connecting exponential equations and their graphs

This is a Geogebra applet created by Steve Phelps in which you construct the graph of an exponential function by placing the asymptote, the y-intercept and one other point. You then type in what you think the graph of your equation ought to be. The equation you type in is graphed so you can see if you're right.

Graph Explorer

This applet allows you to graph multiple functions in different colors and to zoom in and out easily. A nice feature is that you can define parameters (e.g., m and b in y = mx + b) and then vary their values using a slider and watch the graph change.

Algebra Arrows

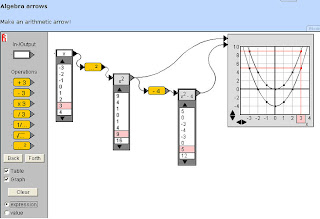
This is a very cool applet from WisWeb for illustrating the building of an algebraic function and the relationship between tabular and graphical representations of the function. I didn't find much in the way of instructions on the website (much of which is in Dutch, though there is a more limited English version), but try this to build graphs and tables for y = x, y = x^2, and y = x^2 - 4:

1. Drag an In-/Output box to the main area of the applet and type an x in it.

2. Check both the Table and Graph check boxes. A table of values will appear with your In-/Output box and a blank graph will appear.

3. Drag the yellow "squared" operator into the main area.

4. Drag the arrow on the In-/Output box until it connects with the tiny gray dot on the operator box.

5. Add another In-/Output box and drag the operator arrow to connect with the little gray dot on this new box. The table below this box now shows the squares of all the values in the table below your original In-Output box.

6. Drag the arrow on the new In-/Output box over to the graph and the graph of y = x^2 appears. (Click and drag on the graph to see different portions of the graph and use the arrows to change the scales on the axes.) If you click one of the numbers in the tables, the corresponding number in the other table and the corresponding point on the graph will be highlighted.

7. Drag the subtraction operator into the main area and change its 3 to a 4.

8. Connect the x^2 In-/Output box to the subtraction operator.

9. Add another In-/Output box and connect the subtraction operator to it to see a table of values for x^2 - 4. Connect this new In-/Output box to the graph to show its graph as well as the original graph.