Domain of a Function defined by a Composition

I created this GeoGebra

applet to help with visualization of the domain of a function defined by a composition.

Snail's Trail Quilt Square

I created this GeoGebra applet based on a quilt square pattern to use in a precalculus class as a visual introduction to the sum of an infinite geometric series. A nice accompaniment is this applet from Irina Boyadzhiev. I also created a Desmos activity with a focus on asking questions which incorporates these two applets.

Visualizing radians

Sam Shah shared a GeoGebra applet created by a colleage of his which does a beautiful job of demonstrating what a radian is. He wrote about it here. I made minor modifications, mostly so that the word radian doesn't actually appear. Here's that slightly modified version.

Exponential Models Card Sort

Thanks to the ever-innovative-and-tuned-in-to-what-teachers-would-love-to-have Desmos team, I've created an online version of a card sort that I originally developed in paper form to help precalculus students think carefully about the meaning of the parameters in various forms of exponential equations. See this blog post for more detail on the context in which I use this.

Variation on John Golden's GeoGebra Ferris Wheel

I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.

We had a great discussion in precalculus class today based on a single randomly generated wheel. We went wherever student questions and answers took us and ended up covering lots of ground. The particularly interesting stuff from my perspective came when those who saw the graph as a shifted sine wave were fighting it out with those who saw it as a shifted cosine wave and those who saw it as a flipped cosine wave. Finally lots of people were seeing lots of ways that they might write an equation for a sinusoidal wave. At the very end of class we generated a new wheel and everyone tried to write a function to go along with it. Class was over and people were pleading, "Please--try my equation!"

Asymptotes of Rational Functions.

Asymptotes of Rational Functions is a GeoGebra construction designed to help people explore the relationship between the equation of a rational function and its graph. You choose the rational function you'd like to explore. Here's a story of something neat that happened when I used it in class.

Finding Equations of Polynomial and Rational Functions

I created this activity with Desmos. Graphs of several polynomial and rational functions are provided. The goal is to find the equation of each. It's self-checking in that when you type in the right equation your graph will match the given graph.

Observe and Ask

This simple Desmos sketch is designed to elicit observations and questions that will lead naturally to an introduction of the ideas of domain and range and an exploration of power functions. I show it to a class without any explanation and as I move the a-slider I ask for questions (which I write on the board, but don't answer). If students want the k-slider moved or if they want to see a particular value of a or k, I oblige. Eventually I ask students to begin trying to answer some of the questions and see where that takes us.

Puzzle

Can you figure out how the p and q sliders control the lines? To check your answer, try typing in equations of the lines (in terms of p and q) in the blank rows underneath the sliders and see if the lines that your equations produce match the lines that are already there. (When you've found something that works--but not before, that's cheating!--you can scroll down to rows below the blank ones to see if your equations are the same as the ones that were actually used to produce the lines.)

Operations on functions graphically

A.B. Cron has created a series of GeoGebra applets that demonstrate operations on functions graphically. You can enter any two functions (f and g) and then, from their graphs, determine points that will be on the graph of, for example, h = f + g. After plotting a number of points, you can check the box to show the graph of h to check your work. The adding functions applet has links to the applets for subtracting, multiplying, dividing, and composition.

(Links updated 7/30/2016)

Finding logs

This is a clean, simple applet by Michael Borcherds that provides practice finding logs. It keeps track of how many you got right on the first try and how much time you've spent. To restart the count, refresh the page.

Inverse functions graphically

Taylor Russell's inverse function applet provides a very nice visualization of the fact that the graph of an inverse function is obtained by switching the x- and y-coordinates of every point. You input the original function, so it is extremely flexible. As an added bonus, you can also plot the reciprocal function and see that it is not the same as the inverse. I used this applet in combination with Emily Alman's Joe the Math Guy comic for my most successful introduction to inverse functions ever.

Mathmo

Mathmo is a review tool for A-level maths developed by the NRICH project at the University of Cambridge. It is advertised to work in Chrome, Safari, and on mobile devices. There are questions on wide range of topics in a typical American high school curriculum, though the range of question types within a topic is very limited. In some topics (logarithms, for example) there are a few different types of questions, but in most there is a single question type where just the specifics (numbers, functions, etc.) vary. You can ask for random questions from the wide range of syllabus topics or can choose your own specific topics to build up a set of questions. You work the problems on paper (or in your head) and then push the check answer button to compare your answer with the given one. If you want several questions on the same topic, you can add the topic multiple times to your question list or can click the new button from within a particular question.

I did experience a couple of minor bugs. Sometimes, the first time you look at a question you see the code rather than the mathematical notation. Clicking (or tapping) the question changes the code to notation. The description says that the color of the question changes once you indicate whether you got the question right or wrong. I didn't experience that either on the iPad or in Chrome.

Ferris Wheel

This is a full-featured and beautifully designed GeoGebra applet from John Golden that allows students to practice fitting parameters to a cosine function which models the height of a ferris wheel car above the ground as a function of time. You can watch the ferris wheel spin as the height curve is generated and it provides an endless source of practice since you can always generate a new ferris wheel.

Napier's Gift

I was inspired by the first chapter of Eli Maor's e:The Story of a Number to create this GeoGebra applet designed to help the user discover how to simplify the process of finding a quotient by subtracting exponents. The idea is both to introduce students to logarithms (though they are never mentioned explicitly) and to help students understand why they were so heralded when they were introduced. The applet is also posted on GeoGebraTube.

Indiana Puzzle Quilt

This applet was inspired by a quilt square my mother-in-law made. It provides a nice way of visualizing the  the sum of an infinite geometric series.
Check out the pattern in some real quilts, too!

Update 1/5/2017: See the Snail's Trail Quilt Square

Rational Function Graphs

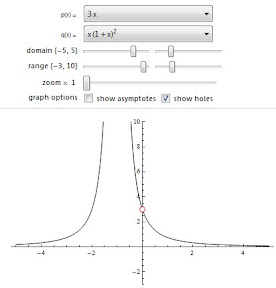Use this demonstration from the Wolfram Demonstrations Project to explore the graphs of rational functions. Predict whether the function will have any holes and then check "show holes" to see if you're right. (To interact with it online you'll need to download and install Wolfram's free CDF Player.)

Law of Sines and Law of Cosines

This applet can be used to provide convincing evidence for the Laws of Sines and Cosines and, once the laws are established, to provide practice problems. I like to begin by showing just the measure of an angle and its opposite side and turning on the help to see the ratio of the sine of the angle to the length of the opposite side. Repeating this for the other two angle-side pairs and dragging the vertices around to create new triangles suggests that these three ratios are always equal for a given triangle. Similarly, sliding the dot along the line reveals the expressions and calculations associated with the Law of Cosines. To provide practice problems, turn off the help and choose any three of the six possible pieces of information. Drag a vertex (or two or three) to create a new triangle. Check answers by revealing the remaining angle and side measures.

Vectors in the Ocean

This applet provides an introduction to the vector equation of a line in the context of a boat traveling in the ocean. You specify the position vector and the velocity vector and then watch how the boat moves and the equation changes as the time changes. (Making the ocean visible sets the mood, but turning it off makes it easier to see what's happening!)

Graph of a quartic

In this GeoGebra applet, you graph a quartic by setting the values of the four zeros and the leading coefficient. The coordinates of all relative extrema are shown.