Intuitive Notion of the Limit - One-Sided Limits

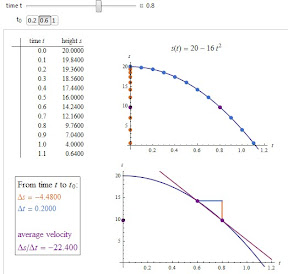
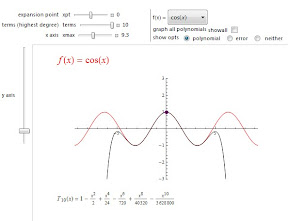
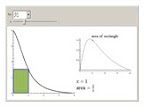
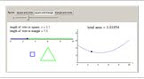
This applet, which is part of Marc Renault's GeoGebra Calculus Applets collection, provides an intuitive introduction to the idea of a limit of a function as x approaches c from the right, left, or both.

The red, green, and blue lines along the x-axis, y-axis and the function which shrink as you decrease δ help with the visualization of motion along the function toward the point where x = c and the corresponding motion toward the limiting values on the axes. Choose from the good library of example functions that are included or enter your own. (I like to start with my own rational function which looks linear but actually has an unseen hole to emphasize from the very beginning the difference between the value of a function and its limit at a point.)

When I used this with a class for the first time, my students asked to see the examples with "Exploding" in the title and they reacted audibly to the motion of the green lines on the y-axis as the function approached its asymptote. My experience has been that when introduced to the idea of limits on a graph there are always a few students who have a lot of difficulty visualizing the various ways in which certain things approach approach other things, and starting with this applet seemed to really help.

Indiana Puzzle Quilt

This applet was inspired by a quilt square my mother-in-law made. It provides a nice way of visualizing the  the sum of an infinite geometric series.
Check out the pattern in some real quilts, too!

Update 1/5/2017: See the Snail's Trail Quilt Square

Constructing the Area of a Circle

A beautifully designed applet that walks you through finding the area of a circle by dividing it up into sectors and rearranging them to form a shape which becomes a rectangle as the number of sectors goes to infinity. I recommend using it in conjunction with Steven Strogatz's fabulous article, "Take it to the Limit". (If you like this, you might also like this applet which approaches the same problem in a slightly different way.)

The Volume of a Watermelon

To introduce the idea of finding the volume of a solid of revolution, have students think about finding the volume of a watermelon.

Sketch the Graph of an Antiderivative

Given a graph of f ' and a few points on the graph of f, find the graph of f.

Derivative Matching Game

From a set of graphs, choose function and derivative pairs (or triads, if you'd like to practice with both first and second derivatives.)

Velocity of a Falling Object

Use this demonstration from the Wolfram Demonstrations Project to explore average and instantaneous velocity for a falling object. (To interact with it online you'll need to download and install Wolfram's free CDF Player.)

Graphs of Taylor Polynomials

Use this demonstration from the Wolfram Demonstrations Project to explore Taylor polynomial approximations to a variety of functions. (To interact with it online you'll need to download and install Wolfram's free CDF Player.)

Max-Min Demonstrations from the Wolfram Demonstrations Project

These are some of the demonstrations from the Wolfram Demonstrations Project that illustrate classic Calculus I optimization problems. To interact with these online you'll need to download and install Wolfram's free CDF Player.

Introduction to Rectilinear Motion

Watch a particle moving along a line and figure out how to draw the corresponding position vs. time and velocity vs. time graphs. It is possible to change the position function by typing "s(x) = " followed by whatever function you'd like in the input line. (You can also access this applet on GeoGebraTube.)



Download the Geogebra file which is the basis for this applet

Calculus Grapher

A nice applet from the PhET project at the University of Colorado enabling you to quickly "sketch" a graph of a particular shape and to see graphs of its derivative and integral.

GeoGebra Calculus Applets Project

"

This is a collection of applets created by Marc Renault of Shippensburg University. Marc's "goal is to make a complete library of applets for Calculus I that are suitable for in-class demonstrations and/or student exploration."

Introduction to Area Under a Curve

In this applet from the GeoGebra Calculus Applets Project, you enter a function and position endpoints to see what the value of the integral is.

The Area Function

This applet from the GeoGebra Calculus Applets Project provides a way to explore the area function. The default integrand can be changed by right-clicking on the curve.

Chain Rule Flashcards

I created these flashcards using Quizlet to help students practice using the chain rule.

Practice with the chain rule when the outside function is ln x

Practice with the chain rule when a power function is plugged into a trig function

Practice with the chain rule when a trig function is plugged into a power function

Turning a Circle into a Rectangle

After reading Steven Strogatz's column Take It to the Limit, I developed this animation (using GeoGebra) of Strogatz's diagram which shows why the formula for the area of circle is what it is, and also provides an approximation for π.

Riemann Sums

A GeoGebra applet from The Lawrenceville School's Equation Plotter collection which draws and calculates area approximations for any function you enter.

Derivative Plotter

This applet from the Flash Mathlets collection by Barbara Kaskosz invites you to draw (with your mouse) a derivative of any of the included example functions or one you enter yourself. You can check your graph by dragging a slider to have the applet draw the actual graph of the derivative.

Accumulated Rate of Change and Antiderivatives

This applet from the Flash Mathlets collection by Barbara Kaskosz includes graphs of a bunch of sample rate of change functions. For each, as you drag a slider, you see what the associated population (i.e., antiderivative) would look like. You can also input your own rate of change function and initial condition. What's more, you can draw your own  function, specify an initial condition, draw what you think the associated antiderivative would look like, and then check your antiderivative by moving the slider to see the applet draw the antiderivative.

Definite Integral as an Area Accumulator

This clear, elegant applet from the Flash Mathlets collection by Barbara Kaskosz shows the integral as an area accumulator for a few simple functions.