Introduction to Point-Slope Form

I created this Desmos activity to help students understand point-slope form of a linear equation, both how it relates to the equation for calculating the slope between two points and why it might be useful even if you're already good at slope-intercept form. It also introduces the idea of calling the change in x by the name h.

Evaluating Inverse Trig Expressions

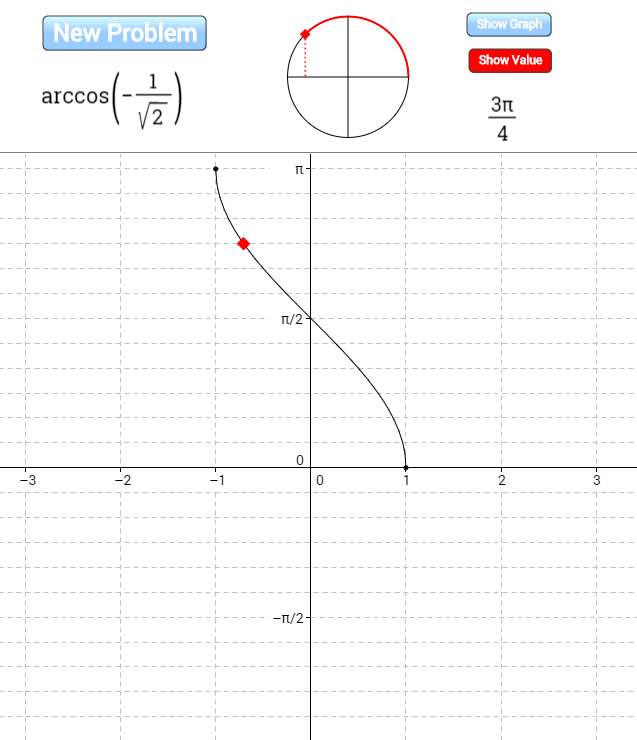I created this applet on GeoGebraTube to help students practice evaluating inverse trig functions of special angles by visualizing both the unit circle and the graph of the inverse trig function.

Variation on John Golden's GeoGebra Ferris Wheel

I love John Golden's GeoGebra Ferris Wheel, which he's written about here and I've written about here. I also love how GeoGebraTube makes it so easy to start with the great work of someone else and create a variation on it. Here's my variation on John's creation for a user who's slightly more experienced with transformations and with sine and cosine functions. Rather than asking the user to come up with parameters for a given function, it requires the user to come up with the whole function. I also added the option to hide the actual function so that the user could begin by thinking about what it would look like.

We had a great discussion in precalculus class today based on a single randomly generated wheel. We went wherever student questions and answers took us and ended up covering lots of ground. The particularly interesting stuff from my perspective came when those who saw the graph as a shifted sine wave were fighting it out with those who saw it as a shifted cosine wave and those who saw it as a flipped cosine wave. Finally lots of people were seeing lots of ways that they might write an equation for a sinusoidal wave. At the very end of class we generated a new wheel and everyone tried to write a function to go along with it. Class was over and people were pleading, "Please--try my equation!"

Asymptotes of Rational Functions.

Asymptotes of Rational Functions is a GeoGebra construction designed to help people explore the relationship between the equation of a rational function and its graph. You choose the rational function you'd like to explore. Here's a story of something neat that happened when I used it in class.

Finding Equations of Polynomial and Rational Functions

I created this activity with Desmos. Graphs of several polynomial and rational functions are provided. The goal is to find the equation of each. It's self-checking in that when you type in the right equation your graph will match the given graph.

Inverse functions graphically

Taylor Russell's inverse function applet provides a very nice visualization of the fact that the graph of an inverse function is obtained by switching the x- and y-coordinates of every point. You input the original function, so it is extremely flexible. As an added bonus, you can also plot the reciprocal function and see that it is not the same as the inverse. I used this applet in combination with Emily Alman's Joe the Math Guy comic for my most successful introduction to inverse functions ever.

Ferris Wheel

This is a full-featured and beautifully designed GeoGebra applet from John Golden that allows students to practice fitting parameters to a cosine function which models the height of a ferris wheel car above the ground as a function of time. You can watch the ferris wheel spin as the height curve is generated and it provides an endless source of practice since you can always generate a new ferris wheel.

Spinning Out Sine and Cosine

A nice animation from the Wolfram Demonstrations Project showing the relationship between a circle and the graphs of sine and cosine. I like the way the cosine graph is show on its side. I'm going to try using it (after editing it in Mathematica to remove the sine and cosine labels) as an introduction both to the unit circle and the trig graphs. It looks like a good candidate for the technique of showing an animation with no commentary and then asking for student questions, writing them on the board, and asking for answers to/discussion of any of the questions.

Contour Plots

This is a well-designed tool for creating and exploring contour plots. It has nice customization options and you can save your plots in a wide range of formats. It comes from Bulgaria and Macedonia's Computational Science and Engineering Program.

Sketch the Graph of an Antiderivative

Given a graph of f ' and a few points on the graph of f, find the graph of f.

Find the equation of a line

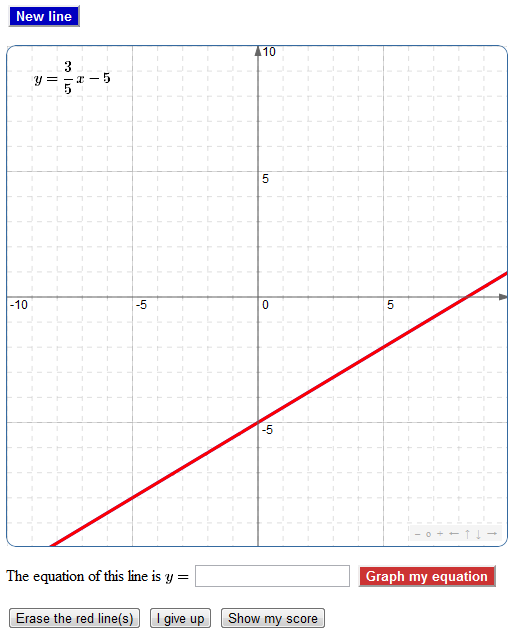In this applet a line is randomly generated and the user enters what she thinks the equation is. Her equation is then graphed for comparison with the original. There is a scoring mechanism incorporated as well.

This is my first applet created with JSXGraph , which looks quite promising (though it does require learning Javascript.)

Particularly helpful to me in developing this were Dr. Carol Fisher's Reference on JSXGraph Commands and the convert-to-math script  in use at interactive mathematics. (The latter enables the user to enter the equation using standard calculator notation.) I also found the javascript tutorial at w3schools.com a very useful introduction to javascript.

The application uses MathJax to produce nice mathematical notation.

Rational Function Graphs

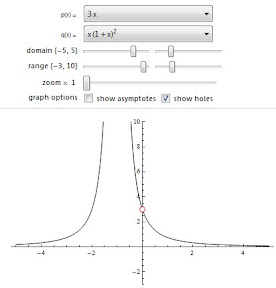Use this demonstration from the Wolfram Demonstrations Project to explore the graphs of rational functions. Predict whether the function will have any holes and then check "show holes" to see if you're right. (To interact with it online you'll need to download and install Wolfram's free CDF Player.)

Polar and Rectangular Coordinates

Use this demonstration from the Wolfram Demonstrations Project to explore the relationship between polar and rectangular coordinates. (To interact with it online you'll need to download and install Wolfram's free CDF Player.)

Calculus Grapher

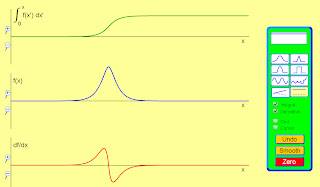A nice applet from the PhET project at the University of Colorado enabling you to quickly "sketch" a graph of a particular shape and to see graphs of its derivative and integral.

Vectors in the Ocean

This applet provides an introduction to the vector equation of a line in the context of a boat traveling in the ocean. You specify the position vector and the velocity vector and then watch how the boat moves and the equation changes as the time changes. (Making the ocean visible sets the mood, but turning it off makes it easier to see what's happening!)

WolframAlpha

Type in, for example, an equation you want to solve, a function you want to graph or the names of two cities. You will want to keep playing. This video by Robert Talbert gives some ideas about how a math teacher or student might begin exploring.

Graph of a quartic

In this GeoGebra applet, you graph a quartic by setting the values of the four zeros and the leading coefficient. The coordinates of all relative extrema are shown.

Writing Equations for Sine and Cosine Functions

This applet I created with GeoGebra has 40 problems, which get progressively more difficult, in which the student must write an equation for a graph which is a stretch and/or translation of a sine/cosine graph. To check whether an equation is correct, the student types in the equation and looks at whether the graphs match up.

Finding the equation of a parabola

This is an applet I created using Geogebra in which the user is asked to enter the equation of randomly generated parabola. The equation entered is graphed for comparison to the target parabola.

Blank Axes for Trig Graphs

Blank axes designed to make it easy to create standard trig graphs for insertion into word processing documents. The full power of Geogebra is behind it. To copy the graph you've made, choose "Graphics View to Clipboard" from the Edit menu.